Gerak yang dibicarakan dalam bagian ini adalah gerak yang dialami benda pada sebuah lintasan berbentuk garis lurus.(sebut saja jalan raya).
Berbicara masalah gerak tentu ada banyak yang berhubungan dengan gerak salah satunya adalah
Mengukur jarak
tempuh, waktu tempuh, dan kecepatan rata-rata suatu benda yang bergerak dapat
dilakukan dengan rumus fisika kinematika. Berikut ulasannya...!
- Kinematika adalah cabang fisika yang mempelajari gerak dengan menghiraukan penyebab gerak. Mengenai penyebab gerak akan dibahas dalam Dinamika.
- Kecepatan didefinisikan sebagai perubahan kedudukan setiap satuan waktu.
- Gerak Lurus Beaturan (GLB) adalah suatu gerak lurus yang mempunyai kecepatan konstan. Maka nilai percepatannya adalah a = 0. Gerakan GLB berbentuk linear dan nilai kecepatannya adalah hasil bagi jarak dengan waktu yang ditempuh.
- Gerak Lurus Beraturan (GLB)
Gerak Lurus Beraturan (GLB) adalah suatu gerak lurus yang mempunyai kecepatan konstan. Maka nilai percepatannya adalah a = 0. Gerakan GLB berbentuk linear dan nilai kecepatannya adalah hasil bagi jarak dengan waktu yang ditempuh.
Rumus:

Dengan ketentuan:
 = Jarak yang ditempuh (m, km)
= Jarak yang ditempuh (m, km)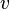 = Kecepatan (km/jam, m/s)
= Kecepatan (km/jam, m/s)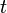 = Waktu tempuh (jam, sekon)
= Waktu tempuh (jam, sekon)
Catatan:
- Untuk mencari jarak yang ditempuh, rumusnya adalah
 .
. - Untuk mencari waktu tempuh, rumusnya adalah
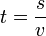 .
. - Untuk mencari kecepatan, rumusnya adalah
 .
.
Kecepatan rata-rata
Rumus:

Contoh soal:
Pengukuran Jarak yang Ditempuh
Ekha mengendarai sepeda motor dengan kecepatan rata-rata 80 km/jam. Ia berangkat dari kota Denpasar menuju kota Singaraja pukul 07.00. Jika Ia tiba di kota Singaraja Pukul 10.00
Berapa Km-kah jarak yang telah ditempuh Ekha ?
Jawaban :
Rumus jarak tempuh
Berapa Km-kah jarak yang telah ditempuh Ekha ?
Jawaban :
Rumus jarak tempuh

Waktu yang ditempuh = waktu tiba – waktu berangkat
= Pukul 10.00 – Pukul 07.00
= 3 jam
= Pukul 10.00 – Pukul 07.00
= 3 jam
Jarak yang ditempuh = kecepatan X waktu
= 80 km/jam X 3 jam
= 240 km
Jadi Ekha menempuh jarak 240 km dari Denpasar ke Singaraja.
= 80 km/jam X 3 jam
= 240 km
Jadi Ekha menempuh jarak 240 km dari Denpasar ke Singaraja.
Pengukuran Waktu yang Ditempuh
Jarak A – B 80 km. Ekha berangkat ke B dengan mobil pukul 08.00.
Kecepatan rata-rata 40 km/jam.
a. Berapa lama waktu tempuh yang dibutuhkan oleh Ekha untuk sampai ke B ?
b. Pukul Berapakah Ekha tiba di B?
Kecepatan rata-rata 40 km/jam.
a. Berapa lama waktu tempuh yang dibutuhkan oleh Ekha untuk sampai ke B ?
b. Pukul Berapakah Ekha tiba di B?
Jawaban :
a. Rumus menghitung waktu tempuh =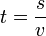 atau
atau
a. Rumus menghitung waktu tempuh =
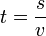 atau
atau
= Jarak : kecepatan
= 80 km : 40 km/jam
= 2 jam
Jadi Ekha memerlukan waktu untuk menempuh jarak A – B adalah
2 jam
= 80 km : 40 km/jam
= 2 jam
Jadi Ekha memerlukan waktu untuk menempuh jarak A – B adalah
2 jam
b. Ekha tiba di B = Waktu keberangkatan + waktu tempuh
= pukul 08.00 + 2 jam
= 10.00
Jadi Ekha tiba di B pukul 10.00
= 10.00
Jadi Ekha tiba di B pukul 10.00
Pengukuran Kecepatan Rata-rata
Jarak dari kota Singaraja ke Denpasar 210 Km. B'gigs mengendarai mobil berangkat
dari Singaraja pukul 07.00 dan tiba di Denpasar pukul 10.00. Berapakah kecepatan rata-rata B'gigs mengendarai mobil ?
dari Singaraja pukul 07.00 dan tiba di Denpasar pukul 10.00. Berapakah kecepatan rata-rata B'gigs mengendarai mobil ?
Jawaban :
Sebelum kita menghitung kecepatan rata-rata kita harus menentukan waktu yang digunakan oleh B'gigsl yaitu
= Tiba – berangkat
= pukul 10.00 – pukul 07.00
= 3jam
Jadi waktu yang digunakan oleh B'gigs adalah 3 jam.
= pukul 10.00 – pukul 07.00
= 3jam
Jadi waktu yang digunakan oleh B'gigs adalah 3 jam.
Barulah kita menentukan kecepatan rata-rata B'gigs mengendarai mobil.
Rumus kecepatan rata-rata =  atau
atau
 atau
atau
= jarak : waktu tempuh
= 210 km : 3 jam
= 70 km/jam
Jadi B'gigs mengendarai mobil dengan kecepatan rata-rata 70 km/jam.
= 210 km : 3 jam
= 70 km/jam
Jadi B'gigs mengendarai mobil dengan kecepatan rata-rata 70 km/jam.
- Gerak Lurus Berubah Beraturan
Gerak lurus berubah beraturan adalah gerak yang lintasannya berupa garis lurus dengan kecepatannya yang berubah beraturan.
Percepatannya bernilai konstan/tetap.
Rumus GLBB ada 3, yaitu:
Dengan ketentuan:
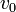 = Kecepatan awal (m/s)
= Kecepatan awal (m/s) = Kecepatan akhir (m/s)
= Kecepatan akhir (m/s)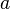 = Percepatan (m/s2)
= Percepatan (m/s2) = Jarak yang ditempuh (m)
= Jarak yang ditempuh (m)
Gerak vertikal ke atas
Benda dilemparkan secara vertikal, tegak lurus terhadap bidang horizontal ke atas dengan kecepatan awal tertentu. Arah gerak benda dan arah percepatan gravitasi berlawanan, gerak lurus berubah beraturan diperlambat.
Peluru akan mencapai titik tertinggi apabila Vt sama dengan nol.
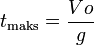

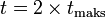

Keterangan:
- Kecepatan awal= Vo
- Kecepatan benda di suatu ketinggian tertentu= Vt
- Percepatan /Gravitasi bumi: g
- Tinggi maksimum: h
- Waktu benda mencapai titik tertinggi: t maks
- Waktu ketika benda kembali ke tanah: t
Gerak vertikal ke bawah
Benda dilemparkan tegak lurus bidang horizontal arahnya ke bawah.
Arah percepatan gravitasi dan arah gerak benda searah, merupakan gerak lurus berubah beraturan dipercepat.


Keterangan:
- Vo = kecepatan awal
- Vt = kecepatan pada ketinggian tertentu dari tanah
- g = gravitasi bumi
- h = jarak yang telah ditempuh secara vertikal
- t = waktu
Gerak jatuh bebas
Benda dikatakan jatuh bebas apabila benda:
- Memiliki ketinggian tertentu (h) dari atas tanah.
- Benda tersebut dijatuhkan tegak lurus bidang horizontal tanpa kecepatan awal.
Selama bergerak ke bawah, benda dipengaruhi oleh percepatan gravitasi bumi (g) dan arah kecepatan/gerak benda searah, merupakan gerak lurus berubah beraturan dipercepat.
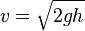
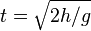
Keterangan:
- v = kecepatan di permukaan tanah
- g = gravitasi bumi
- h = tinggi dari permukaan tanah
- t = lama benda sampai di tanah
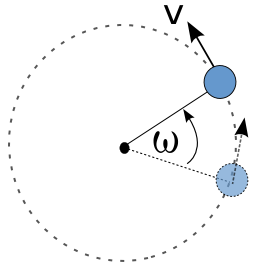
- Gerak melingkar
Gerak dengan lintasan berupa lingkaran.
Dari diagram di atas, diketahui benda bergerak sejauh ω° selama  sekon, maka benda dikatakan melakukan perpindahan sudut.
sekon, maka benda dikatakan melakukan perpindahan sudut.
 sekon, maka benda dikatakan melakukan perpindahan sudut.
sekon, maka benda dikatakan melakukan perpindahan sudut.
Benda melalukan 1 putaran penuh. Besar perpindahan linear adalah  atau keliling lingkaran. Besar perpindahan sudut dalam 1 putaran penuh adalah
atau keliling lingkaran. Besar perpindahan sudut dalam 1 putaran penuh adalah  radian atau 360°.
radian atau 360°.
 atau keliling lingkaran. Besar perpindahan sudut dalam 1 putaran penuh adalah
atau keliling lingkaran. Besar perpindahan sudut dalam 1 putaran penuh adalah  radian atau 360°.
radian atau 360°.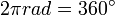

Perpindahan sudut, kecepatan sudut, dan percepatan sudut [sunting]
Perpindahan sudut adalah posisi sudut benda yang bergerak secara melingkar dalam selang waktu tertentu.
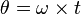
Keterangan:
 = perpindahan sudut (rad)
= perpindahan sudut (rad) = kecepatan sudut (rad/s)
= kecepatan sudut (rad/s)- t = waktu (sekon)
Kecepatan sudut rata-rata ( ): perpindahan sudut per selang waktu.
): perpindahan sudut per selang waktu.
 ): perpindahan sudut per selang waktu.
): perpindahan sudut per selang waktu.
Percepatan sudut rata-rata ( ): perubahan kecepatan sudut per selang waktu.
): perubahan kecepatan sudut per selang waktu.
 ): perubahan kecepatan sudut per selang waktu.
): perubahan kecepatan sudut per selang waktu.
 : Percepatan sudut (rad/s2)
: Percepatan sudut (rad/s2)Percepatan sentripetal [sunting]
Arah percepatan sentripetal selalu menuju ke pusat lingkaran.
Percepatan sentripetal tidak menambah kecepatan, melainkan hanya untuk mempertahankan benda agar tetap bergerak melingkar.
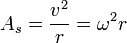
Keterangan:
- r : jari-jari benda/lingkaran
- As: percepatan sentripetal (rad/s2)
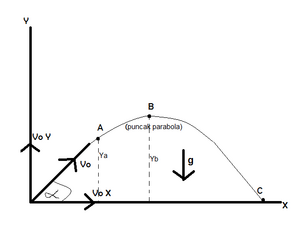
- Gerak parabola
Gerak parabola adalah gerak yang membentuk sudut tertentu terhadap bidang horizontal. Pada gerak parabola, gesekan diabaikan, dan gaya yang bekerja hanya gaya berat/percepatan gravitasi.
Pada titik awal,


Pada titik A (t = ta):

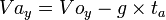
Letak/posisi di A:


Titik tertinggi yang bisa dicapai (B):
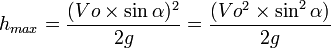
Waktu untuk sampai di titik tertinggi (B) (tb):
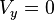

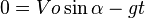

Jarak mendatar/horizontal dari titik awal sampai titik B (Xb):
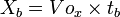
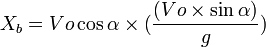

Jarak vertikal dari titik awal ke titik B (Yb):


Waktu untuk sampai di titik C:
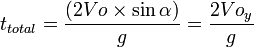
Jarak dari awal bola bergerak sampai titik C:

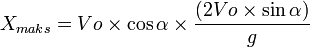
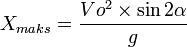
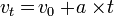

Tidak ada komentar:
Posting Komentar